WannierBerri advanced tutorial - Fermi surface and Fermi sea calculation of the Berry curvature dipole
author: Jae-Mo Lihm (jaemo.lihm@gmail.com)
The Berry curvature dipole (BCD) is the dipole of the Berry curvature in the reciprocal space. BCD has attracted considerable attention, partially because it contributes to the nonlinear Hall effect.
In WannierBerri, there are two ways to compute this quantity: the Fermi surface integral and the Fermi sea integral:
Formally, one can show that the two methods give identical results using partial integration:
The integral is zero because the Brillouin zone has no boundary.
However, in practice, there are numerical differences between the two methods. In this tutorial, we compare the Fermi sea and Fermi surface integral methods for the BCD using the chiral tight-binding model and the ab-initio tight-binding model of ferroelectric GeTe.
[1]:
# Preliminary (Do only once)
%load_ext autoreload
%autoreload 2
# Set environment variables - not mandatory but recommended
import os
os.environ['OPENBLAS_NUM_THREADS'] = '1'
os.environ['MKL_NUM_THREADS'] = '1'
import numpy as np
import scipy
import matplotlib.pyplot as plt
import wannierberri as wberri
from wannierberri import calculators as calc
# This block is needed if you run this cell for a second time
# because one cannot initiate two parallel environments at a time
try:
parallel.shutdown()
except NameError:
pass
parallel = wberri.Parallel(num_cpus=16, progress_step_percent=10)
initializing ray with {'num_cpus': 16}
2025-05-13 16:35:59,595 INFO worker.py:1879 -- Started a local Ray instance. View the dashboard at http://127.0.0.1:8267
Model 1: Chiral tight-binding model
Model, band structure
The model is taken from T. Yoda et al, “Orbital Edelstein Effect as a Condensed-Matter Analog of Solenoids”, Nano Lett. 18, 2, 916–920 (2018) https://arxiv.org/abs/1706.07702
The system is a honeycomb lattice with two orbitals per unit cell with an AA stacking (i.e. an AA stacked 2d hexagonal boron nitride). The original model contains in-plance nearest-neighbor hopping (hop1), vertical hopping (hopz_vert), and chiral inter-layer hopping (hopz_left and hopz_right). Here, we additionally add onsite energy difference (delta) and in-plane next-nearest-neighbor hopping (hop2 and phi). Nonzero phi breaks the time-reversal symmetry.
When we set phi=0, the model has time-reversal symmetry and C3z symmetry. In total, there are 6 symmetry operations.
[2]:
import wannierberri.models
# Initiate a tight-binding model (wannierberri.models.Chiral uses PythTB)
model_Chiral_left = wannierberri.models.Chiral(delta=2., hop1=1., hop2=0.3, phi=0, hopz_left=0.2, hopz_right=0.0, hopz_vert=0)
# Initialize WannierBerri system object
system = wberri.System_PythTB(model_Chiral_left)
print("=" * 40)
# Set symmetry from the generators.
system.set_pointgroup(symmetry_gen=["TimeReversal", "C3z"])
print("Number of symmetry operations: ", system.pointgroup.size)
number of wannier functions: 2
R=0 found at position(s) [[10]]
shape of Ham_R = (21, 2, 2)
Real-space lattice:
[[1. 0. 0. ]
[0.5 0.8660254 0. ]
[0. 0. 1. ]]
Number of wannier functions: 2
Number of R points: 21
Recommended size of FFT grid [3 3 3]
Reading the system from PythTB finished successfully
========================================
Number of symmetry operations: 6
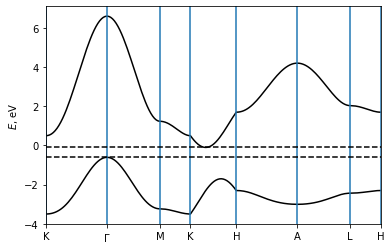
Now, we plot the band structure along a k-point path that passes the high-symmetry k points. We use the plot_path_fat method to plot the band structure.
The energy can be accessed via path_result.get_data("Energy", iband). The valence band maximum is at the Gamma point, while the conduction band minimum on the K-H line.
Figure taken from T. Yoda et al, Nano Lett. 18, 2, 916–920 (2018).
[ ]:
path = wberri.Path(
system,
nodes=[
[2/3, 1/3, 0.], # K
[0., 0., 0.], # Gamma
[1/2, 0., 0.], # M
[2/3, 1/3, 0.], # K
[2/3, 1/3, 0.5], # H
[0., 0., 0.5], # A
[1/2, 0., 0.5], # L
[2/3, 1/3, 0.5], # H
],
labels=["K","$\Gamma$","M","K", "H", "A", "L", "H"],
length=50
)
calculators = {
"tabulate": calc.TabulatorAll(
{"Energy": calc.tabulate.Energy()},
ibands=np.arange(system.num_wann),
mode="path",
)
}
path_result = wberri.run(
system,
grid=path,
calculators=calculators,
parallel=parallel,
print_Kpoints = False,
)
path_result = path_result.results["tabulate"]
Starting run()
Using the follwing calculators :
############################################################
'tabulate' : <wannierberri.calculators.tabulate.TabulatorAll object at 0x776ec8114f20> :
TabulatorAll - a pack of all k-resolved calculators (Tabulators)
Includes the following tabulators :
--------------------------------------------------
"Energy" : <wannierberri.calculators.tabulate.Energy object at 0x776f080f3e00> : calculator not described
--------------------------------------------------
############################################################
Calculation along a path - checking calculators for compatibility
tabulate <wannierberri.calculators.tabulate.TabulatorAll object at 0x776ec8114f20>
All calculators are compatible
Symmetrization switched off for Path
Grid is regular
The set of k points is a Path() with 184 points and labels {0: 'K', 33: '$\\Gamma$', 62: 'M', 79: 'K', 104: 'H', 137: 'A', 166: 'L', 183: 'H'}
generating K_list
Done
Done, sum of weights:184.0
processing 184 K points : using 1 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
<>:13: SyntaxWarning: invalid escape sequence '\G'
<>:13: SyntaxWarning: invalid escape sequence '\G'
/tmp/ipykernel_98527/3984238173.py:13: SyntaxWarning: invalid escape sequence '\G'
labels=["K","$\Gamma$","M","K", "H", "A", "L", "H"],
/home/stepan/github/wannier-berri/wannierberri/grid/path.py:163: UserWarning: symmetry is not used for a tabulation along path
warnings.warn("symmetry is not used for a tabulation along path")
time for processing 184 K-points on 1 processes: 0.7157 ; per K-point 0.0039 ; proc-sec per K-point 0.0039
time1 = 0.0020780563354492188
Totally processed 184 K-points
run() finished
[4]:
e_vbm = np.amax(path_result.get_data("Energy", 0))
e_cbm = np.amin(path_result.get_data("Energy", 1))
print(f"Valence band maximum : {e_vbm:6.3f}")
print(f"Conduction band minimum: {e_cbm:6.3f}")
print("VBM k point: ", path_result.kpoints[np.argmax(path_result.get_data("Energy", 0))])
print("CBM k point: ", path_result.kpoints[np.argmin(path_result.get_data("Energy", 1))])
fig = path_result.plot_path_fat(path, close_fig=False, show_fig=False)
ax = fig.get_axes()[0]
ax.axhline(e_vbm, c="k", ls="--")
ax.axhline(e_cbm, c="k", ls="--")
plt.show(fig)
Valence band maximum : -0.606
Conduction band minimum: -0.099
VBM k point: [0. 0. 0.]
CBM k point: [0.66666667 0.33333333 0.16 ]
Berry curvature dipole
[5]:
from wannierberri.smoother import FermiDiracSmoother
efermi = np.linspace(-2.0, 1.0, 101, True)
# efermi = np.linspace(e_vbm - 0.5, e_cbm + 0.5, 301, True)
kwargs = dict(
Efermi=efermi,
kwargs_formula={"external_terms": False},
smoother=FermiDiracSmoother(efermi, T_Kelvin=1200, maxdE=8)
)
calculators = {
'berry_dipole_fermi_sea': calc.static.BerryDipole_FermiSea(**kwargs),
'berry_dipole_fermi_surface': calc.static.BerryDipole_FermiSurf(**kwargs),
'dos': calc.static.DOS(Efermi=efermi,),
}
Compare calculations using the full k-point grid and the irreducible grid. This can be done using the use_irred_kpt argument of wberri.run.
You can find the following two lines in the output: K_list contains 1000 Irreducible points(100.0%) out of initial 10x10x10=1000 grid K_list contains 172 Irreducible points(17.2%) out of initial 10x10x10=1000 grid
These lines show that using symmetry can speed up calculation by 1000 / 172 ~ 6 times. This speedup corresponds to the 6 symmetry operations. Check that the BCD calculated from the two grids are identical.
[6]:
grid = wberri.Grid(system, NK=20, NKFFT=2)
print("=" * 40)
print("Calculation using the full k-point grid")
result_full_grid = wberri.run(
system,
grid=grid,
calculators=calculators,
parallel=parallel,
print_Kpoints = False,
use_irred_kpt = False,
)
print("=" * 40)
print("Calculation using the irreducible k-point grid")
result_irr_grid = wberri.run(
system,
grid=grid,
calculators=calculators,
parallel=parallel,
print_Kpoints = False,
use_irred_kpt = True,
)
========================================
Calculation using the full k-point grid
Starting run()
Using the follwing calculators :
############################################################
'berry_dipole_fermi_sea' : <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x776f0812c080> : Berry curvature dipole (dimensionless)
| With Fermi sea integral. Eq(29) in `Ref <https://www.nature.com/articles/s41524-021-00498-5>`__
| Output: :math:`D_{\beta\delta} = \int [dk] \partial_\beta \Omega_\delta f`
'berry_dipole_fermi_surface' : <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x776ec04c1ee0> : Berry curvature dipole (dimensionless)
| With Fermi surface integral. Eq(8) in `Ref <https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.115.216806>`__
| Output: :math:`D_{\beta\delta} = -\int [dk] v_\beta \Omega_\delta f'`
'dos' : <wannierberri.calculators.static.DOS object at 0x776ec04c20f0> : Density of states
############################################################
Calculation on grid - checking calculators for compatibility
berry_dipole_fermi_sea <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x776f0812c080>
berry_dipole_fermi_surface <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x776ec04c1ee0>
dos <wannierberri.calculators.static.DOS object at 0x776ec04c20f0>
All calculators are compatible
Grid is regular
The set of k points is a Grid() with NKdiv=[10 10 10], NKFFT=[2 2 2], NKtot=[20 20 20]
generating K_list
Done in 0.003509998321533203 s
K_list contains 1000 Irreducible points(100.0%) out of initial 10x10x10=1000 grid
Done, sum of weights:1.0000000000000007
processing 1000 K points : using 1 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
time for processing 1000 K-points on 1 processes: 4.0077 ; per K-point 0.0040 ; proc-sec per K-point 0.0040
time1 = 0.08731341361999512
Totally processed 1000 K-points
run() finished
========================================
Calculation using the irreducible k-point grid
Starting run()
Using the follwing calculators :
############################################################
'berry_dipole_fermi_sea' : <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x776f0812c080> : Berry curvature dipole (dimensionless)
| With Fermi sea integral. Eq(29) in `Ref <https://www.nature.com/articles/s41524-021-00498-5>`__
| Output: :math:`D_{\beta\delta} = \int [dk] \partial_\beta \Omega_\delta f`
'berry_dipole_fermi_surface' : <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x776ec04c1ee0> : Berry curvature dipole (dimensionless)
| With Fermi surface integral. Eq(8) in `Ref <https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.115.216806>`__
| Output: :math:`D_{\beta\delta} = -\int [dk] v_\beta \Omega_\delta f'`
'dos' : <wannierberri.calculators.static.DOS object at 0x776ec04c20f0> : Density of states
############################################################
Calculation on grid - checking calculators for compatibility
berry_dipole_fermi_sea <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x776f0812c080>
berry_dipole_fermi_surface <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x776ec04c1ee0>
dos <wannierberri.calculators.static.DOS object at 0x776ec04c20f0>
All calculators are compatible
Grid is regular
The set of k points is a Grid() with NKdiv=[10 10 10], NKFFT=[2 2 2], NKtot=[20 20 20]
generating K_list
Done in 0.003713846206665039 s
excluding symmetry-equivalent K-points from initial grid
Done in 0.013213872909545898 s
K_list contains 172 Irreducible points(17.2%) out of initial 10x10x10=1000 grid
Done, sum of weights:1.0000000000000007
processing 172 K points : using 1 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
time for processing 172 K-points on 1 processes: 0.7134 ; per K-point 0.0041 ; proc-sec per K-point 0.0041
time1 = 0.014747858047485352
Totally processed 172 K-points
run() finished
[164]:
dir_string = ["D_xx", "D_yy", "D_zz"]
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
for label, res in zip(["Full grid", "Irr. grid"], [result_full_grid, result_irr_grid]):
data_fsurf = res.results['berry_dipole_fermi_surface'].data
data_fsea = res.results['berry_dipole_fermi_sea'].data
for i in range(3):
if label == "Full grid":
fmt = f"C{i}-"
else:
fmt = "k--"
axes[0].plot(efermi, data_fsurf[:, i, i], fmt, label=label + " " + dir_string[i])
axes[1].plot(efermi, data_fsea[:, i, i], fmt, label=label + " " + dir_string[i])
axes[0].set_title("Fermi surface")
axes[1].set_title("Fermi sea")
for ax in axes:
ax.axhline(0, c="k", lw=1)
ax.set_xlabel("Fermi level (eV)")
ax.set_ylabel("Berry curvature dipole")
axes[1].legend()
plt.tight_layout()
plt.show()
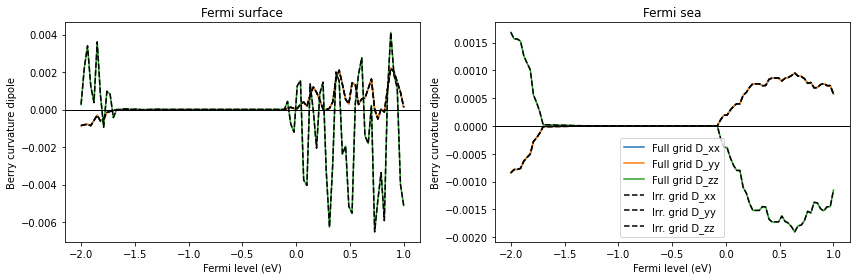
From now on, we use the irreducible k-point grid, which is the default in wberri.run.
[7]:
grid = wberri.Grid(system, NK=20, NKFFT=2)
result = wberri.run(
system,
grid=grid,
calculators=calculators,
parallel=parallel,
print_Kpoints = False,
)
Starting run()
Using the follwing calculators :
############################################################
'berry_dipole_fermi_sea' : <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x776f0812c080> : Berry curvature dipole (dimensionless)
| With Fermi sea integral. Eq(29) in `Ref <https://www.nature.com/articles/s41524-021-00498-5>`__
| Output: :math:`D_{\beta\delta} = \int [dk] \partial_\beta \Omega_\delta f`
'berry_dipole_fermi_surface' : <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x776ec04c1ee0> : Berry curvature dipole (dimensionless)
| With Fermi surface integral. Eq(8) in `Ref <https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.115.216806>`__
| Output: :math:`D_{\beta\delta} = -\int [dk] v_\beta \Omega_\delta f'`
'dos' : <wannierberri.calculators.static.DOS object at 0x776ec04c20f0> : Density of states
############################################################
Calculation on grid - checking calculators for compatibility
berry_dipole_fermi_sea <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x776f0812c080>
berry_dipole_fermi_surface <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x776ec04c1ee0>
dos <wannierberri.calculators.static.DOS object at 0x776ec04c20f0>
All calculators are compatible
Grid is regular
The set of k points is a Grid() with NKdiv=[10 10 10], NKFFT=[2 2 2], NKtot=[20 20 20]
generating K_list
Done in 0.0019369125366210938 s
excluding symmetry-equivalent K-points from initial grid
Done in 0.010958194732666016 s
K_list contains 172 Irreducible points(17.2%) out of initial 10x10x10=1000 grid
Done, sum of weights:1.0000000000000007
processing 172 K points : using 1 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
time for processing 172 K-points on 1 processes: 0.6542 ; per K-point 0.0038 ; proc-sec per K-point 0.0038
time1 = 0.014677047729492188
Totally processed 172 K-points
run() finished
[8]:
data_fsurf = result.results['berry_dipole_fermi_surface'].data
data_fsea = result.results['berry_dipole_fermi_sea'].data
print("Shape of data: ", data_fsurf.shape)
print("Maximum value for each components (Fermi surface): ")
print(np.linalg.norm(data_fsurf, axis=0))
print("Maximum value for each components (Fermi sea): ")
print(np.linalg.norm(data_fsea, axis=0))
Shape of data: (101, 3, 3)
Maximum value for each components (Fermi surface):
[[6.21590176e-03 8.59577012e-19 5.06603030e-18]
[1.16684168e-18 6.21590176e-03 1.23671954e-18]
[8.40279503e-19 2.24111542e-19 2.01147852e-02]]
Maximum value for each components (Fermi sea):
[[4.68803509e-03 6.93422151e-19 1.39090780e-17]
[2.63355804e-18 4.68803509e-03 1.58054575e-18]
[3.17500857e-19 7.41680867e-20 9.37607018e-03]]
[9]:
dir_string = ["D_xx", "D_yy", "D_zz"]
for i in range(3):
plt.plot(efermi, data_fsurf[:, i, i], c=f"C{i}", label="Fermi surface " + dir_string[i])
plt.plot(efermi, data_fsea[:, i, i], c=f"C{i}", label="Fermi sea " + dir_string[i], ls="--")
# plt.plot(efermi, result.results['dos'].data, "k-")
plt.axhline(0, c="k", lw=1)
plt.xlabel("Fermi level")
plt.ylabel("Berry curvature dipole")
plt.axvline(e_vbm, c="k", lw=1, ls="--")
plt.axvline(e_cbm, c="k", lw=1, ls="--")
plt.legend()
plt.show()
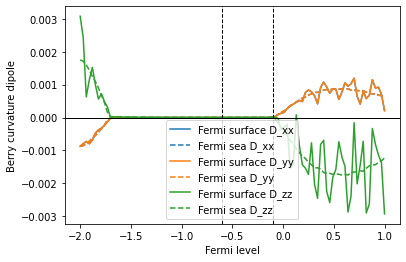
The trace of the BCD tensor should be zero due to a topological reason (see footnote 2 of S.Tsirkin et al, PRB 97, 035158 (2018) for details).
The Fermi sea formula for the BCD tensor is explicitly traceless at every k point: this fact can be proven from the definition of the Fermi sea formula using
In contrast, tracelessness is not explicit in the Fermi surface formula. The trace of the BCD tensor becomes zero only after summing over the full Brillouin zone due to the cancellation of contributions from all the k points.
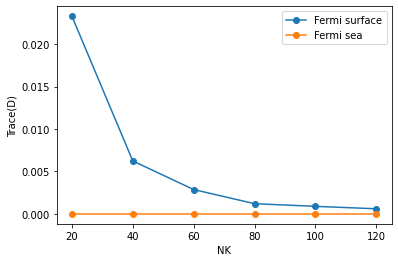
Therefore, in numerical calculations using a finite number of k points, only the Fermi sea formula, not the Fermi surface formula, gives a zero trace. The trace will converge to 0 in the Fermi surface case as one makes the k-point grid denser.
[10]:
data_fsurf_trace = np.trace(data_fsurf, axis1=1, axis2=2)
data_fsea_trace = np.trace(data_fsea, axis1=1, axis2=2)
plt.plot(efermi, data_fsurf_trace, label="Fermi surface")
plt.plot(efermi, data_fsea_trace, label="Fermi sea")
plt.axhline(0, c="k", lw=1, zorder=1)
plt.xlabel("Fermi level")
plt.ylabel("Trace(D)")
plt.axvline(e_vbm, c="k", lw=1, ls="--")
plt.axvline(e_cbm, c="k", lw=1, ls="--")
plt.legend()
plt.show()

Try to calculate the Berry curvature dipole using the two methods for various grid sizes and see how they converge. Also, check that the trace of Berry curvature dipole indeed converges to 0 for both methods.
(NK=120 will be enough to see convergence.)
[11]:
data_fsurf_all = {}
data_fsea_all = {}
[12]:
for nk in [20, 40, 60, 80]:
grid = wberri.Grid(system, NK=nk)
result = wberri.run(
system,
grid=grid,
calculators=calculators,
parallel=parallel,
print_Kpoints = False,
)
data_fsurf_all[nk] = result.results['berry_dipole_fermi_surface'].data
data_fsea_all[nk] = result.results['berry_dipole_fermi_sea'].data
Minimal symmetric FFT grid : [3 3 3]
Starting run()
Using the follwing calculators :
############################################################
'berry_dipole_fermi_sea' : <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x776f0812c080> : Berry curvature dipole (dimensionless)
| With Fermi sea integral. Eq(29) in `Ref <https://www.nature.com/articles/s41524-021-00498-5>`__
| Output: :math:`D_{\beta\delta} = \int [dk] \partial_\beta \Omega_\delta f`
'berry_dipole_fermi_surface' : <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x776ec04c1ee0> : Berry curvature dipole (dimensionless)
| With Fermi surface integral. Eq(8) in `Ref <https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.115.216806>`__
| Output: :math:`D_{\beta\delta} = -\int [dk] v_\beta \Omega_\delta f'`
'dos' : <wannierberri.calculators.static.DOS object at 0x776ec04c20f0> : Density of states
############################################################
Calculation on grid - checking calculators for compatibility
berry_dipole_fermi_sea <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x776f0812c080>
berry_dipole_fermi_surface <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x776ec04c1ee0>
dos <wannierberri.calculators.static.DOS object at 0x776ec04c20f0>
All calculators are compatible
Grid is regular
The set of k points is a Grid() with NKdiv=[5 5 5], NKFFT=[4 4 4], NKtot=[20 20 20]
generating K_list
Done in 0.0006937980651855469 s
excluding symmetry-equivalent K-points from initial grid
Done in 0.004553794860839844 s
K_list contains 23 Irreducible points(18.4%) out of initial 5x5x5=125 grid
Done, sum of weights:1.0000000000000002
processing 23 K points : using 1 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
time for processing 23 K-points on 1 processes: 0.2797 ; per K-point 0.0122 ; proc-sec per K-point 0.0122
time1 = 0.002042531967163086
Totally processed 23 K-points
run() finished
Minimal symmetric FFT grid : [3 3 3]
Starting run()
Using the follwing calculators :
############################################################
'berry_dipole_fermi_sea' : <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x776f0812c080> : Berry curvature dipole (dimensionless)
| With Fermi sea integral. Eq(29) in `Ref <https://www.nature.com/articles/s41524-021-00498-5>`__
| Output: :math:`D_{\beta\delta} = \int [dk] \partial_\beta \Omega_\delta f`
'berry_dipole_fermi_surface' : <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x776ec04c1ee0> : Berry curvature dipole (dimensionless)
| With Fermi surface integral. Eq(8) in `Ref <https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.115.216806>`__
| Output: :math:`D_{\beta\delta} = -\int [dk] v_\beta \Omega_\delta f'`
'dos' : <wannierberri.calculators.static.DOS object at 0x776ec04c20f0> : Density of states
############################################################
Calculation on grid - checking calculators for compatibility
berry_dipole_fermi_sea <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x776f0812c080>
berry_dipole_fermi_surface <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x776ec04c1ee0>
dos <wannierberri.calculators.static.DOS object at 0x776ec04c20f0>
All calculators are compatible
Grid is regular
The set of k points is a Grid() with NKdiv=[10 10 10], NKFFT=[4 4 4], NKtot=[40 40 40]
generating K_list
Done in 0.0025098323822021484 s
excluding symmetry-equivalent K-points from initial grid
Done in 0.014392375946044922 s
K_list contains 172 Irreducible points(17.2%) out of initial 10x10x10=1000 grid
Done, sum of weights:1.0000000000000007
processing 172 K points : using 1 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
time for processing 172 K-points on 1 processes: 1.8689 ; per K-point 0.0109 ; proc-sec per K-point 0.0109
time1 = 0.015810012817382812
Totally processed 172 K-points
run() finished
Minimal symmetric FFT grid : [3 3 3]
Starting run()
Using the follwing calculators :
############################################################
'berry_dipole_fermi_sea' : <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x776f0812c080> : Berry curvature dipole (dimensionless)
| With Fermi sea integral. Eq(29) in `Ref <https://www.nature.com/articles/s41524-021-00498-5>`__
| Output: :math:`D_{\beta\delta} = \int [dk] \partial_\beta \Omega_\delta f`
'berry_dipole_fermi_surface' : <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x776ec04c1ee0> : Berry curvature dipole (dimensionless)
| With Fermi surface integral. Eq(8) in `Ref <https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.115.216806>`__
| Output: :math:`D_{\beta\delta} = -\int [dk] v_\beta \Omega_\delta f'`
'dos' : <wannierberri.calculators.static.DOS object at 0x776ec04c20f0> : Density of states
############################################################
Calculation on grid - checking calculators for compatibility
berry_dipole_fermi_sea <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x776f0812c080>
berry_dipole_fermi_surface <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x776ec04c1ee0>
dos <wannierberri.calculators.static.DOS object at 0x776ec04c20f0>
All calculators are compatible
Grid is regular
The set of k points is a Grid() with NKdiv=[20 20 20], NKFFT=[3 3 3], NKtot=[60 60 60]
generating K_list
Done in 0.017724037170410156 s
excluding symmetry-equivalent K-points from initial grid
Done in 0.10371255874633789 s
K_list contains 1342 Irreducible points(16.78%) out of initial 20x20x20=8000 grid
Done, sum of weights:1.00000000000001
processing 1342 K points : using 1 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
time for processing 1342 K-points on 1 processes: 8.7973 ; per K-point 0.0066 ; proc-sec per K-point 0.0066
time1 = 0.12499642372131348
Totally processed 1342 K-points
run() finished
Minimal symmetric FFT grid : [3 3 3]
Starting run()
Using the follwing calculators :
############################################################
'berry_dipole_fermi_sea' : <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x776f0812c080> : Berry curvature dipole (dimensionless)
| With Fermi sea integral. Eq(29) in `Ref <https://www.nature.com/articles/s41524-021-00498-5>`__
| Output: :math:`D_{\beta\delta} = \int [dk] \partial_\beta \Omega_\delta f`
'berry_dipole_fermi_surface' : <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x776ec04c1ee0> : Berry curvature dipole (dimensionless)
| With Fermi surface integral. Eq(8) in `Ref <https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.115.216806>`__
| Output: :math:`D_{\beta\delta} = -\int [dk] v_\beta \Omega_\delta f'`
'dos' : <wannierberri.calculators.static.DOS object at 0x776ec04c20f0> : Density of states
############################################################
Calculation on grid - checking calculators for compatibility
berry_dipole_fermi_sea <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x776f0812c080>
berry_dipole_fermi_surface <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x776ec04c1ee0>
dos <wannierberri.calculators.static.DOS object at 0x776ec04c20f0>
All calculators are compatible
Grid is regular
The set of k points is a Grid() with NKdiv=[20 20 20], NKFFT=[4 4 4], NKtot=[80 80 80]
generating K_list
Done in 0.017277956008911133 s
excluding symmetry-equivalent K-points from initial grid
Done in 0.10439825057983398 s
K_list contains 1342 Irreducible points(16.78%) out of initial 20x20x20=8000 grid
Done, sum of weights:1.00000000000001
processing 1342 K points : using 1 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
time for processing 1342 K-points on 1 processes: 14.3822 ; per K-point 0.0107 ; proc-sec per K-point 0.0107
time1 = 0.1406095027923584
Totally processed 1342 K-points
run() finished
[208]:
ic = 0
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
nklist = sorted(list(data_fsurf_all.keys()))
for nk in nklist:
c = f"C{ic}"
axes[0].plot(efermi, data_fsurf_all[nk][:, 0, 0], c=c, label=f"NK={nk}")
axes[1].plot(efermi, data_fsea_all[nk][:, 0, 0], c=c, label=f"NK={nk}")
ic += 1
axes[0].set_title("Fermi surface")
axes[1].set_title("Fermi sea")
for ax in axes:
ax.axhline(0, c="k", lw=1)
ax.set_ylim([-1.5e-3, 1.5e-3])
ax.set_xlabel("Fermi level (eV)")
ax.set_ylabel("Berry curvature dipole")
axes[1].legend()
plt.tight_layout()
plt.show()
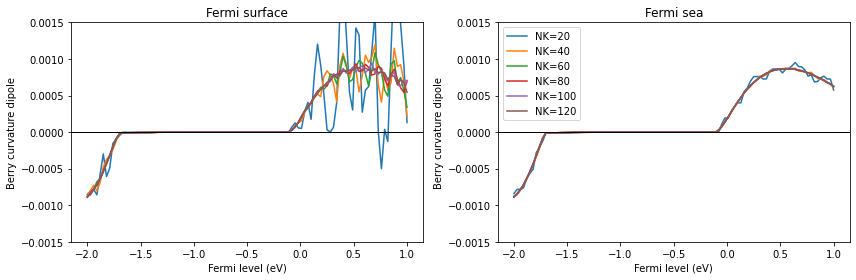
[13]:
ic = 0
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
for nk in sorted(list(data_fsurf_all.keys())):
c = f"C{ic}"
axes[0].plot(efermi, np.trace(data_fsurf_all[nk], axis1=1, axis2=2), c=c, label=f"NK={nk}")
axes[1].plot(efermi, np.trace(data_fsea_all[nk], axis1=1, axis2=2), c=c, label=f"NK={nk}")
ic += 1
axes[0].set_title("Fermi surface")
axes[1].set_title("Fermi sea")
for ax in axes:
ax.axhline(0, c="k", lw=1)
ax.set_ylim([-1.5e-3, 1.5e-3])
ax.set_xlabel("Fermi level (eV)")
ax.set_ylabel("Trace of Berry curvature dipole")
axes[1].legend()
plt.tight_layout()
plt.show()
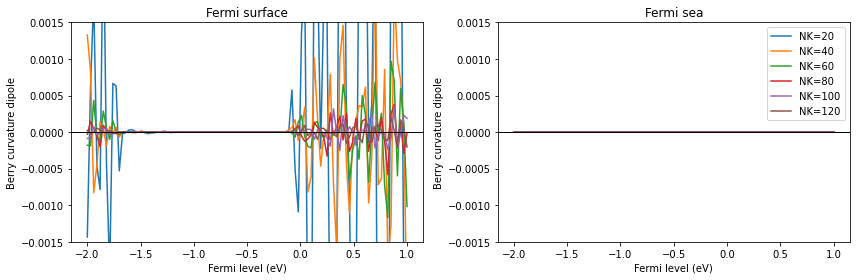
[14]:
nklist = sorted(list(data_fsurf_all.keys()))
plt.plot(nklist, [np.linalg.norm(np.trace(data_fsurf_all[nk], axis1=1, axis2=2)) for nk in nklist], "o-", label="Fermi surface")
plt.plot(nklist, [np.linalg.norm(np.trace(data_fsea_all[nk], axis1=1, axis2=2)) for nk in nklist], "o-", label="Fermi sea")
plt.legend()
plt.xlabel("NK")
plt.ylabel("Trace(D)")
# plt.yscale("log")
plt.show()
Model 2: Ferroelectric germanium telluride (α-GeTe)
The second model is an ab-initio tighit-binding model of ferroelectric GeTe. This material has a rhombohedrally distorted rocksalt structure where the Te atom is shifted from the center of the unit cell along the [111] direction.
Figure taken from H. Wang et al, npj Computational Materials, 6, 7 (2020).
We load the system from a Wannier90 output. We set symmetry using the set_symmetry_from_structure method, which calls spglib to automatically determine the symmetry of the system.
We also symmetrize the system. See data_GeTe/GeTe.win file and check that the initial projections are correct. For details, refer to the symmetrization tutorial.
[2]:
system_GeTe = wberri.System_w90("../data_GeTe/GeTe", berry=True)
system_GeTe.set_structure([[0., 0., 0.], [0.4688262167, 0.4688262167, 0.4688262167]], ["Ge", "Te"])
system_GeTe.set_symmetry_from_structure()
system_GeTe.symmetrize(
proj=["Ge:s", "Ge:p", "Te:s", "Te:p"],
atom_name=["Ge", "Te"],
positions=[[0., 0., 0.], [0.4688262167, 0.4688262167, 0.4688262167]],
soc=False,
)
kwargs for mmn are {'read_npz': True, 'write_npz': True}
calling w90 file with ../data_GeTe/GeTe, mmn, tags=['data', 'neighbours', 'G'], read_npz=True, write_npz=True, kwargs={'npar': 32}
kwargs for eig are {'read_npz': True, 'write_npz': True}
calling w90 file with ../data_GeTe/GeTe, eig, tags=['data'], read_npz=True, write_npz=True, kwargs={}
Reading restart information from file ../data_GeTe/GeTe.chk :
Time to read .chk : 0.001489877700805664
setting Rvec
expjphase1 (1, 8, 8)
Real-space lattice:
[[ 2.11676981 -1.22211762 3.64031036]
[ 0. 2.44423524 3.64031036]
[-2.11676981 -1.22211762 3.64031036]]
Number of wannier functions: 8
Number of R points: 63
Recommended size of FFT grid [3 3 3]
---------- CRYSTAL STRUCTURE ----------
Cell vectors in angstroms:
Vectors of DFT cell
a0 = 2.1168 -1.2221 3.6403
a1 = 0.0000 2.4442 3.6403
a2 = -2.1168 -1.2221 3.6403
---------- SPACE GROUP -----------
Space group: R3m1' (# 160.66)
Number of symmetries: 12 (mod. lattice translations)
### 1
rotation : | 1 0 0 |
| 0 1 0 |
| 0 0 1 |
gk = [kx, ky, kz]
translation : [ 0.0000 0.0000 0.0000 ]
axis: [ 0.042527 -0.776177 0.629079] ; angle = 0 , inversion : False, time reversal: False
### 2
rotation : | 1 0 0 |
| 0 1 0 |
| 0 0 1 |
gk = [-kx, -ky, -kz]
translation : [ 0.0000 0.0000 0.0000 ]
axis: [ 0.042527 -0.776177 0.629079] ; angle = 0 , inversion : False, time reversal: True
### 3
rotation : | 0 1 0 |
| 0 0 1 |
| 1 0 0 |
gk = [ky, kz, kx]
translation : [ 0.0000 0.0000 0.0000 ]
axis: [-0. -0. 1.] ; angle = -2/3 pi, inversion : False, time reversal: False
### 4
rotation : | 0 1 0 |
| 0 0 1 |
| 1 0 0 |
gk = [-ky, -kz, -kx]
translation : [ 0.0000 0.0000 0.0000 ]
axis: [-0. -0. 1.] ; angle = -2/3 pi, inversion : False, time reversal: True
### 5
rotation : | 0 0 1 |
| 1 0 0 |
| 0 1 0 |
gk = [kz, kx, ky]
translation : [ 0.0000 0.0000 0.0000 ]
axis: [ 0. -0. 1.] ; angle = 2/3 pi, inversion : False, time reversal: False
### 6
rotation : | 0 0 1 |
| 1 0 0 |
| 0 1 0 |
gk = [-kz, -kx, -ky]
translation : [ 0.0000 0.0000 0.0000 ]
axis: [ 0. -0. 1.] ; angle = 2/3 pi, inversion : False, time reversal: True
### 7
rotation : | 0 0 1 |
| 0 1 0 |
| 1 0 0 |
gk = [kz, ky, kx]
translation : [ 0.0000 0.0000 0.0000 ]
axis: [1. 0. 0.] ; angle = 1 pi, inversion : True, time reversal: False
### 8
rotation : | 0 0 1 |
| 0 1 0 |
| 1 0 0 |
gk = [-kz, -ky, -kx]
translation : [ 0.0000 0.0000 0.0000 ]
axis: [1. 0. 0.] ; angle = 1 pi, inversion : True, time reversal: True
### 9
rotation : | 1 0 0 |
| 0 0 1 |
| 0 1 0 |
gk = [kx, kz, ky]
translation : [ 0.0000 0.0000 0.0000 ]
axis: [-0.5 -0.866025 -0. ] ; angle = 1 pi, inversion : True, time reversal: False
### 10
rotation : | 1 0 0 |
| 0 0 1 |
| 0 1 0 |
gk = [-kx, -kz, -ky]
translation : [ 0.0000 0.0000 0.0000 ]
axis: [-0.5 -0.866025 -0. ] ; angle = 1 pi, inversion : True, time reversal: True
### 11
rotation : | 0 1 0 |
| 1 0 0 |
| 0 0 1 |
gk = [ky, kx, kz]
translation : [ 0.0000 0.0000 0.0000 ]
axis: [-0.5 0.866025 0. ] ; angle = 1 pi, inversion : True, time reversal: False
### 12
rotation : | 0 1 0 |
| 1 0 0 |
| 0 0 1 |
gk = [-ky, -kx, -kz]
translation : [ 0.0000 0.0000 0.0000 ]
axis: [-0.5 0.866025 0. ] ; angle = 1 pi, inversion : True, time reversal: True
pos_list: [[0]]
proj: Projection 0.0, 0.0, 0.0:['s'] with 1 Wannier functions on 1 points (1 per site)
orbital = s, num wann per site = 1
pos_list: [[0]]
proj: Projection 0.0, 0.0, 0.0:['p'] with 3 Wannier functions on 1 points (3 per site)
orbital = p, num wann per site = 3
pos_list: [[0]]
proj: Projection 0.4688262167, 0.4688262167, 0.4688262167:['s'] with 1 Wannier functions on 1 points (1 per site)
orbital = s, num wann per site = 1
pos_list: [[0]]
proj: Projection 0.4688262167, 0.4688262167, 0.4688262167:['p'] with 3 Wannier functions on 1 points (3 per site)
orbital = p, num wann per site = 3
new_wann_indices: [0, 1, 2, 3, 4, 5, 6, 7]
orbitals = ['s']
orbitals = ['p']
orbitals = ['s']
orbitals = ['p']
calculating Wannier functions for s at [[0. 0. 0.]]
calculating Wannier functions for p at [[0. 0. 0.]]
calculating Wannier functions for s at [[0.46882622 0.46882622 0.46882622]]
calculating Wannier functions for p at [[0.46882622 0.46882622 0.46882622]]
len(D_wann_list) = 4
D.shape [(0, 12, 1, 1), (0, 12, 3, 3), (0, 12, 1, 1), (0, 12, 3, 3)]
num_wann 8
D_wann_block_indices [[0 1]
[1 4]
[4 5]
[5 8]]
[2]:
<wannierberri.symmetry.sawf.SymmetrizerSAWF at 0x78f34070b0b0>
[ ]:
path = wberri.Path(
system_GeTe,
nodes=[
[0.00000, 0.00000, 0.00000], # GAMMA
[0.50000, 0.00000, 0.00000], # L
[0.62910, 0.62910, 0.24180], # U
[0.50000, 0.50000, 0.00000], # X
[0.00000, 0.00000, 0.00000], # GAMMA
[0.50000, 0.50000, 0.50000], # Z
[0.62910, 0.62910, 0.24180], # U
],
labels=["$\Gamma$","L","U","X", "$\Gamma$", "Z", "U"],
length=50
)
calculators = {
"tabulate": calc.TabulatorAll(
{"Energy": calc.tabulate.Energy()},
ibands=np.arange(system_GeTe.num_wann),
mode="path",
)
}
path_result = wberri.run(
system_GeTe,
grid=path,
calculators=calculators,
parallel=parallel,
print_Kpoints = False,
)
path_result = path_result.results["tabulate"]
Starting run()
Using the follwing calculators :
############################################################
'tabulate' : <wannierberri.calculators.tabulate.TabulatorAll object at 0x78f36331ba10> :
TabulatorAll - a pack of all k-resolved calculators (Tabulators)
Includes the following tabulators :
--------------------------------------------------
"Energy" : <wannierberri.calculators.tabulate.Energy object at 0x78f363c1d8e0> : calculator not described
--------------------------------------------------
############################################################
Calculation along a path - checking calculators for compatibility
tabulate <wannierberri.calculators.tabulate.TabulatorAll object at 0x78f36331ba10>
All calculators are compatible
Symmetrization switched off for Path
Grid is regular
The set of k points is a Path() with 39 points and labels {0: '$\\Gamma$', 7: 'L', 15: 'U', 18: 'X', 26: '$\\Gamma$', 33: 'Z', 38: 'U'}
generating K_list
Done
Done, sum of weights:39.0
processing 39 K points : using 16 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
<>:12: SyntaxWarning: invalid escape sequence '\G'
<>:12: SyntaxWarning: invalid escape sequence '\G'
<>:12: SyntaxWarning: invalid escape sequence '\G'
<>:12: SyntaxWarning: invalid escape sequence '\G'
/tmp/ipykernel_100008/1250455147.py:12: SyntaxWarning: invalid escape sequence '\G'
labels=["$\Gamma$","L","U","X", "$\Gamma$", "Z", "U"],
/tmp/ipykernel_100008/1250455147.py:12: SyntaxWarning: invalid escape sequence '\G'
labels=["$\Gamma$","L","U","X", "$\Gamma$", "Z", "U"],
/home/stepan/github/wannier-berri/wannierberri/grid/path.py:163: UserWarning: symmetry is not used for a tabulation along path
warnings.warn("symmetry is not used for a tabulation along path")
time for processing 39 K-points on 16 processes: 0.9368 ; per K-point 0.0240 ; proc-sec per K-point 0.3843
time1 = 0.00039196014404296875
Totally processed 39 K-points
run() finished
[4]:
# Calculate the VBM and CBM energies using a 30*30*30 grid.
calculators = {
"tabulate": calc.TabulatorAll(
{"Energy": calc.tabulate.Energy()},
ibands=np.arange(system_GeTe.num_wann),
mode="grid",
)
}
grid_energy_result = wberri.run(
system_GeTe,
grid=wberri.Grid(system_GeTe, NK=30),
calculators=calculators,
parallel=parallel,
print_Kpoints = False,
)
grid_energy_result = grid_energy_result.results["tabulate"]
e_vbm_GeTe = np.amax(grid_energy_result.get_data("Energy", 4))
e_cbm_GeTe = np.amin(grid_energy_result.get_data("Energy", 5))
print(f"Valence band maximum : {e_vbm_GeTe:6.3f}")
print(f"Conduction band minimum: {e_cbm_GeTe:6.3f}")
print("VBM k point: ", grid_energy_result.kpoints[np.argmax(grid_energy_result.get_data("Energy", 0))])
print("CBM k point: ", grid_energy_result.kpoints[np.argmin(grid_energy_result.get_data("Energy", 1))])
Minimal symmetric FFT grid : [3 3 3]
Starting run()
Using the follwing calculators :
############################################################
'tabulate' : <wannierberri.calculators.tabulate.TabulatorAll object at 0x78f328046ba0> :
TabulatorAll - a pack of all k-resolved calculators (Tabulators)
Includes the following tabulators :
--------------------------------------------------
"Energy" : <wannierberri.calculators.tabulate.Energy object at 0x78f340119880> : calculator not described
--------------------------------------------------
############################################################
Calculation on grid - checking calculators for compatibility
tabulate <wannierberri.calculators.tabulate.TabulatorAll object at 0x78f328046ba0>
All calculators are compatible
Grid is regular
The set of k points is a Grid() with NKdiv=[10 10 10], NKFFT=[3 3 3], NKtot=[30 30 30]
generating K_list
Done in 0.002313852310180664 s
excluding symmetry-equivalent K-points from initial grid
Done in 0.019689559936523438 s
K_list contains 116 Irreducible points(11.6%) out of initial 10x10x10=1000 grid
Done, sum of weights:1.0000000000000007
processing 116 K points : using 16 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
time for processing 116 K-points on 16 processes: 0.3964 ; per K-point 0.0034 ; proc-sec per K-point 0.0547
time1 = 0.03557586669921875
setting the grid
setting new kpoints
finding equivalent kpoints
collecting
collecting: to_grid : 0.05154585838317871
collecting: TABresult : 0.00046181678771972656
collecting - OK : 0.0520319938659668 (2.4318695068359375e-05)
Totally processed 116 K-points
run() finished
Valence band maximum : 9.225
Conduction band minimum: 9.836
VBM k point: [0.2 0.5 0.76666667]
CBM k point: [0. 0. 0.5]
[5]:
fig = path_result.plot_path_fat(path, close_fig=False, show_fig=False)
ax = fig.get_axes()[0]
ax.axhline(e_vbm_GeTe, c="k", ls="--")
ax.axhline(e_cbm_GeTe, c="k", ls="--")
plt.show(fig)

We compute the BCD tensor for the hole-doped case. (The electron-doped case is much harder to converge due to band crossings near the CBM.)
Try to calculate BCD for various grids and compare the convergence of the two methods. (NK=120 will be enough to see convergence.)
[7]:
from wannierberri import calculators as calc
from wannierberri.smoother import FermiDiracSmoother
efermi = np.linspace(e_vbm_GeTe - 1.5, e_cbm_GeTe, 301, True)
smoother = FermiDiracSmoother(efermi, 300.0)
kwargs = dict(
Efermi=efermi,
smoother=smoother,
)
calculators = {
'berry_dipole_fermi_sea': calc.static.BerryDipole_FermiSea(**kwargs),
'berry_dipole_fermi_surface': calc.static.BerryDipole_FermiSurf(**kwargs),
}
[8]:
data_GeTe_fsurf_all = {}
data_GeTe_fsea_all = {}
for nk in [20, 30, 40, 60, 80, 120]:
grid = wberri.Grid(system_GeTe, NK=nk)
result = wberri.run(
system_GeTe,
grid=grid,
calculators=calculators,
parallel=parallel,
print_Kpoints = False,
)
data_GeTe_fsurf_all[nk] = result.results['berry_dipole_fermi_surface'].dataSmooth
data_GeTe_fsea_all[nk] = result.results['berry_dipole_fermi_sea'].dataSmooth
Minimal symmetric FFT grid : [3 3 3]
Starting run()
Using the follwing calculators :
############################################################
'berry_dipole_fermi_sea' : <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x78f3280848c0> : Berry curvature dipole (dimensionless)
| With Fermi sea integral. Eq(29) in `Ref <https://www.nature.com/articles/s41524-021-00498-5>`__
| Output: :math:`D_{\beta\delta} = \int [dk] \partial_\beta \Omega_\delta f`
'berry_dipole_fermi_surface' : <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x78f3280cbfe0> : Berry curvature dipole (dimensionless)
| With Fermi surface integral. Eq(8) in `Ref <https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.115.216806>`__
| Output: :math:`D_{\beta\delta} = -\int [dk] v_\beta \Omega_\delta f'`
############################################################
Calculation on grid - checking calculators for compatibility
berry_dipole_fermi_sea <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x78f3280848c0>
berry_dipole_fermi_surface <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x78f3280cbfe0>
All calculators are compatible
Grid is regular
The set of k points is a Grid() with NKdiv=[5 5 5], NKFFT=[4 4 4], NKtot=[20 20 20]
generating K_list
Done in 0.00027942657470703125 s
excluding symmetry-equivalent K-points from initial grid
Done in 0.002663135528564453 s
K_list contains 19 Irreducible points(15.2%) out of initial 5x5x5=125 grid
Done, sum of weights:1.0000000000000004
processing 19 K points : using 16 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
time for processing 19 K-points on 16 processes: 0.1912 ; per K-point 0.0101 ; proc-sec per K-point 0.1610
time1 = 0.002107858657836914
Totally processed 19 K-points
run() finished
Minimal symmetric FFT grid : [3 3 3]
Starting run()
Using the follwing calculators :
############################################################
'berry_dipole_fermi_sea' : <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x78f3280848c0> : Berry curvature dipole (dimensionless)
| With Fermi sea integral. Eq(29) in `Ref <https://www.nature.com/articles/s41524-021-00498-5>`__
| Output: :math:`D_{\beta\delta} = \int [dk] \partial_\beta \Omega_\delta f`
'berry_dipole_fermi_surface' : <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x78f3280cbfe0> : Berry curvature dipole (dimensionless)
| With Fermi surface integral. Eq(8) in `Ref <https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.115.216806>`__
| Output: :math:`D_{\beta\delta} = -\int [dk] v_\beta \Omega_\delta f'`
############################################################
Calculation on grid - checking calculators for compatibility
berry_dipole_fermi_sea <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x78f3280848c0>
berry_dipole_fermi_surface <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x78f3280cbfe0>
All calculators are compatible
Grid is regular
The set of k points is a Grid() with NKdiv=[10 10 10], NKFFT=[3 3 3], NKtot=[30 30 30]
generating K_list
Done in 0.0032606124877929688 s
excluding symmetry-equivalent K-points from initial grid
Done in 0.01862955093383789 s
K_list contains 116 Irreducible points(11.6%) out of initial 10x10x10=1000 grid
Done, sum of weights:1.0000000000000007
processing 116 K points : using 16 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
time for processing 116 K-points on 16 processes: 0.6893 ; per K-point 0.0059 ; proc-sec per K-point 0.0951
time1 = 0.010873079299926758
Totally processed 116 K-points
run() finished
Minimal symmetric FFT grid : [3 3 3]
Starting run()
Using the follwing calculators :
############################################################
'berry_dipole_fermi_sea' : <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x78f3280848c0> : Berry curvature dipole (dimensionless)
| With Fermi sea integral. Eq(29) in `Ref <https://www.nature.com/articles/s41524-021-00498-5>`__
| Output: :math:`D_{\beta\delta} = \int [dk] \partial_\beta \Omega_\delta f`
'berry_dipole_fermi_surface' : <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x78f3280cbfe0> : Berry curvature dipole (dimensionless)
| With Fermi surface integral. Eq(8) in `Ref <https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.115.216806>`__
| Output: :math:`D_{\beta\delta} = -\int [dk] v_\beta \Omega_\delta f'`
############################################################
Calculation on grid - checking calculators for compatibility
berry_dipole_fermi_sea <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x78f3280848c0>
berry_dipole_fermi_surface <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x78f3280cbfe0>
All calculators are compatible
Grid is regular
The set of k points is a Grid() with NKdiv=[10 10 10], NKFFT=[4 4 4], NKtot=[40 40 40]
generating K_list
Done in 0.00263214111328125 s
excluding symmetry-equivalent K-points from initial grid
Done in 0.01764655113220215 s
K_list contains 116 Irreducible points(11.6%) out of initial 10x10x10=1000 grid
Done, sum of weights:1.0000000000000007
processing 116 K points : using 16 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
time for processing 116 K-points on 16 processes: 1.0815 ; per K-point 0.0093 ; proc-sec per K-point 0.1492
time1 = 0.012034893035888672
Totally processed 116 K-points
run() finished
Minimal symmetric FFT grid : [3 3 3]
Starting run()
Using the follwing calculators :
############################################################
'berry_dipole_fermi_sea' : <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x78f3280848c0> : Berry curvature dipole (dimensionless)
| With Fermi sea integral. Eq(29) in `Ref <https://www.nature.com/articles/s41524-021-00498-5>`__
| Output: :math:`D_{\beta\delta} = \int [dk] \partial_\beta \Omega_\delta f`
'berry_dipole_fermi_surface' : <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x78f3280cbfe0> : Berry curvature dipole (dimensionless)
| With Fermi surface integral. Eq(8) in `Ref <https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.115.216806>`__
| Output: :math:`D_{\beta\delta} = -\int [dk] v_\beta \Omega_\delta f'`
############################################################
Calculation on grid - checking calculators for compatibility
berry_dipole_fermi_sea <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x78f3280848c0>
berry_dipole_fermi_surface <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x78f3280cbfe0>
All calculators are compatible
Grid is regular
The set of k points is a Grid() with NKdiv=[20 20 20], NKFFT=[3 3 3], NKtot=[60 60 60]
generating K_list
Done in 0.03239083290100098 s
excluding symmetry-equivalent K-points from initial grid
Done in 0.13759541511535645 s
K_list contains 781 Irreducible points(9.76%) out of initial 20x20x20=8000 grid
Done, sum of weights:0.999999999999985
processing 781 K points : using 16 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
time for processing 781 K-points on 16 processes: 4.2053 ; per K-point 0.0054 ; proc-sec per K-point 0.0862
time1 = 0.06903386116027832
Totally processed 781 K-points
run() finished
Minimal symmetric FFT grid : [3 3 3]
Starting run()
Using the follwing calculators :
############################################################
'berry_dipole_fermi_sea' : <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x78f3280848c0> : Berry curvature dipole (dimensionless)
| With Fermi sea integral. Eq(29) in `Ref <https://www.nature.com/articles/s41524-021-00498-5>`__
| Output: :math:`D_{\beta\delta} = \int [dk] \partial_\beta \Omega_\delta f`
'berry_dipole_fermi_surface' : <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x78f3280cbfe0> : Berry curvature dipole (dimensionless)
| With Fermi surface integral. Eq(8) in `Ref <https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.115.216806>`__
| Output: :math:`D_{\beta\delta} = -\int [dk] v_\beta \Omega_\delta f'`
############################################################
Calculation on grid - checking calculators for compatibility
berry_dipole_fermi_sea <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x78f3280848c0>
berry_dipole_fermi_surface <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x78f3280cbfe0>
All calculators are compatible
Grid is regular
The set of k points is a Grid() with NKdiv=[20 20 20], NKFFT=[4 4 4], NKtot=[80 80 80]
generating K_list
Done in 0.018337726593017578 s
excluding symmetry-equivalent K-points from initial grid
Done in 0.1428370475769043 s
K_list contains 781 Irreducible points(9.76%) out of initial 20x20x20=8000 grid
Done, sum of weights:0.999999999999985
processing 781 K points : using 16 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
time for processing 781 K-points on 16 processes: 7.2489 ; per K-point 0.0093 ; proc-sec per K-point 0.1485
time1 = 0.07642436027526855
Totally processed 781 K-points
run() finished
Minimal symmetric FFT grid : [3 3 3]
Starting run()
Using the follwing calculators :
############################################################
'berry_dipole_fermi_sea' : <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x78f3280848c0> : Berry curvature dipole (dimensionless)
| With Fermi sea integral. Eq(29) in `Ref <https://www.nature.com/articles/s41524-021-00498-5>`__
| Output: :math:`D_{\beta\delta} = \int [dk] \partial_\beta \Omega_\delta f`
'berry_dipole_fermi_surface' : <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x78f3280cbfe0> : Berry curvature dipole (dimensionless)
| With Fermi surface integral. Eq(8) in `Ref <https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.115.216806>`__
| Output: :math:`D_{\beta\delta} = -\int [dk] v_\beta \Omega_\delta f'`
############################################################
Calculation on grid - checking calculators for compatibility
berry_dipole_fermi_sea <wannierberri.calculators.static.BerryDipole_FermiSea object at 0x78f3280848c0>
berry_dipole_fermi_surface <wannierberri.calculators.static.BerryDipole_FermiSurf object at 0x78f3280cbfe0>
All calculators are compatible
Grid is regular
The set of k points is a Grid() with NKdiv=[40 40 40], NKFFT=[3 3 3], NKtot=[120 120 120]
generating K_list
Done in 0.20934605598449707 s
excluding symmetry-equivalent K-points from initial grid
Done in 0.926764965057373 s
K_list contains 5761 Irreducible points(9.0%) out of initial 40x40x40=64000 grid
Done, sum of weights:1.0000000000000313
processing 5761 K points : using 16 processes.
# K-points calculated Wall time (sec) Est. remaining (sec)
time for processing 5761 K-points on 16 processes: 32.1959 ; per K-point 0.0056 ; proc-sec per K-point 0.0894
time1 = 0.5219027996063232
Totally processed 5761 K-points
run() finished
[12]:
nk = 20
print("Shape of data: ", data_GeTe_fsurf_all[nk].shape)
print("Maximum value for each components (Fermi surface): ")
print(np.amax(abs(data_GeTe_fsurf_all[nk]), axis=0))
print("Maximum value for each components (Fermi sea): ")
print(np.amax(abs(data_GeTe_fsea_all[nk]), axis=0))
Shape of data: (301, 3, 3)
Maximum value for each components (Fermi surface):
[[5.83625890e-19 4.82033606e-02 8.44858920e-19]
[4.82033606e-02 3.26505102e-19 2.04911009e-19]
[1.35354371e-18 1.59827632e-19 5.74866053e-19]]
Maximum value for each components (Fermi sea):
[[7.63931109e-19 4.51984438e-02 1.34671495e-18]
[4.51984438e-02 3.71736785e-19 5.77229237e-19]
[1.31145095e-18 1.40333414e-19 2.89294300e-19]]
[13]:
ic = 0
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
for nk in sorted(list(data_GeTe_fsurf_all.keys())):
c = f"C{ic}"
axes[0].plot(efermi, data_GeTe_fsurf_all[nk][:, 0, 1], c=c, label=f"NK={nk}")
axes[1].plot(efermi, data_GeTe_fsea_all[nk][:, 0, 1], c=c, label=f"NK={nk}")
ic += 1
axes[0].set_title("Fermi surface")
axes[1].set_title("Fermi sea")
for ax in axes:
ax.axhline(0, c="k", lw=1)
ax.axvline(e_vbm_GeTe, c="k", lw=1, ls="--")
ax.axvline(e_cbm_GeTe, c="k", lw=1, ls="--")
ax.set_ylim([-0.05, 0.05])
ax.set_xlabel("Fermi level (eV)")
ax.set_ylabel("Berry curvature dipole")
axes[1].legend()
plt.tight_layout()
plt.show()
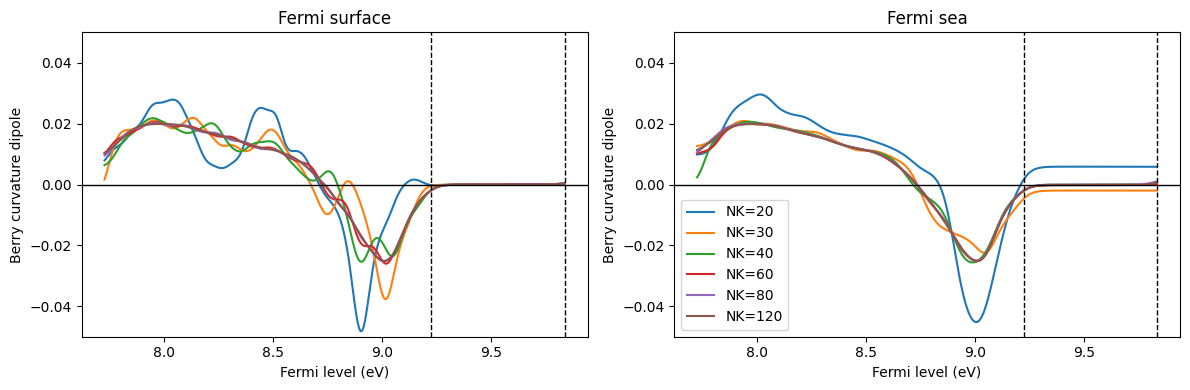
Let us focus on the undoped case: Fermi level between the VBM and the CBM. Then, $:nbsphinx-math:frac{partial}{partial k^a} f_0 (\varepsilon_{n:nbsphinx-math:mathbf{k}}) =0 $ holds so that the BCD is always 0. For the Fermi surface method, the integrand is 0 at every k point, so the integral is also 0. However, for the Fermi sea method, the integrand is not 0, and the integral becomes 0 only due to a calculation.
[14]:
ic = 0
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
for nk in sorted(list(data_GeTe_fsurf_all.keys())):
c = f"C{ic}"
axes[0].plot(efermi, data_GeTe_fsurf_all[nk][:, 0, 1], c=c, label=f"NK={nk}")
axes[1].plot(efermi, data_GeTe_fsea_all[nk][:, 0, 1], c=c, label=f"NK={nk}")
ic += 1
axes[0].set_title("Fermi surface")
axes[1].set_title("Fermi sea")
for ax in axes:
ax.axhline(0, c="k", lw=1)
ax.axvline(e_vbm_GeTe, c="k", lw=1, ls="--")
ax.axvline(e_cbm_GeTe, c="k", lw=1, ls="--")
ax.set_xlabel("Fermi level (eV)")
ax.set_ylabel("Berry curvature dipole")
ax.set_ylim(np.array([-0.01, 0.03]) * 1)
ax.set_xlim([e_vbm_GeTe - 0.1, e_cbm_GeTe + 0.1])
axes[1].legend()
fig.suptitle("zoom around the band gap")
plt.tight_layout()
plt.show()
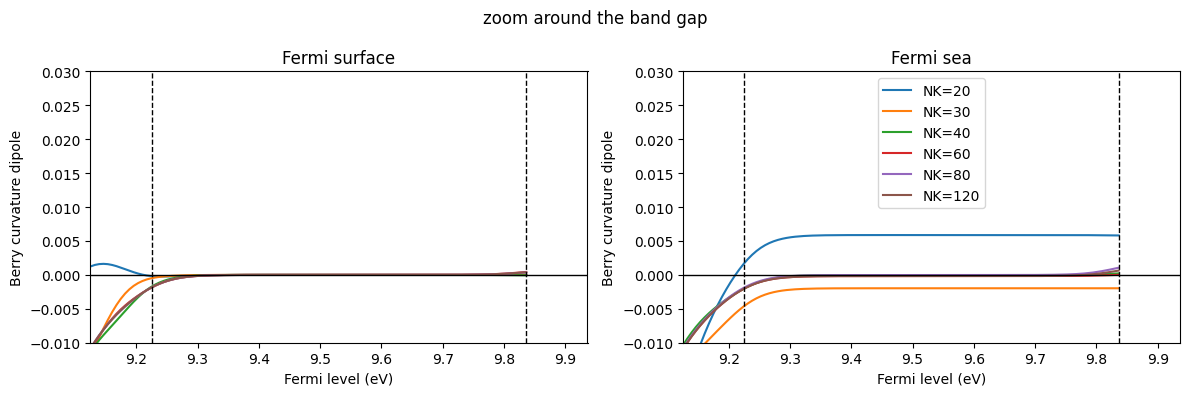
[19]:
# Choose the Fermi level index at the middle of the band gap.
ifermi = np.argmin(np.abs(efermi - (e_vbm_GeTe + e_cbm_GeTe) / 2))
nklist = sorted(list(data_GeTe_fsurf_all.keys()))
print("D_xy for the undoped case")
print("NK : ", nklist)
print("Fermi sea: ", [data_GeTe_fsea_all[nk][ifermi, 0, 1] for nk in nklist])
print("Fermi surface: ", [data_GeTe_fsurf_all[nk][ifermi, 0, 1] for nk in nklist])
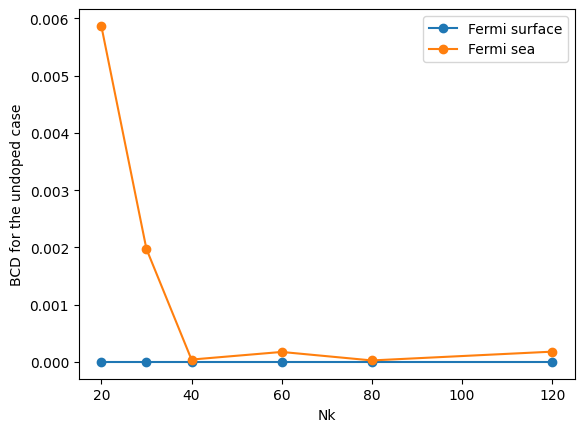
plt.plot(nklist, [abs(data_GeTe_fsurf_all[NK][ifermi, 0, 1]) for NK in nklist], "o-", label="Fermi surface")
plt.plot(nklist, [abs(data_GeTe_fsea_all[NK][ifermi, 0, 1]) for NK in nklist], "o-", label="Fermi sea")
plt.legend()
# plt.yscale("log") # Also try logscale
plt.xlabel("Nk")
plt.ylabel("BCD for the undoped case")
plt.show()
D_xy for the undoped case
NK : [20, 30, 40, 60, 80, 120]
Fermi sea: [np.float64(0.005868797821571347), np.float64(-0.001974244136048048), np.float64(-4.106357261372514e-05), np.float64(-0.00017425364359295427), np.float64(-2.5997303955030933e-05), np.float64(-0.00017942767877330914)]
Fermi surface: [np.float64(0.0), np.float64(0.0), np.float64(0.0), np.float64(0.0), np.float64(0.0), np.float64(0.0)]
Further questions
If you are interested, try to answer the following questions:
What happens if one uses an un-symmetrized model? Does Fermi sea BCD with the Fermi energy inside the gap converge to 0?
What happens if one uses the tetrahedron method?
What happens for the zero-temperature case (you may use
.datainstead of.dataSmooth)?